What You Need to Know to Learn Calculus

What yous need to know before y'all get started: A brief tour of Calculus Pre-Requisites

Last Updated on July 8, 2021

We have previously seen that calculus is ane of the cadre mathematical concepts in car learning that permits united states of america to empathise the internal workings of different machine learning algorithms.

Calculus, in plow, builds on several fundamental concepts that derive from algebra and geometry. The importance of having these fundamentals at manus will go fifty-fifty more of import as we work our mode through more advanced topics of calculus, such as the evaluation of limits and the computation of derivatives, to name a few.

In this tutorial, you will discover several pre-requisites that volition help you piece of work with calculus.

After completing this tutorial, you will know:

• Linear and not-linear functions are central to calculus and auto learning, and many calculus issues involve their employ.
• Fundamental concepts from algebra and trigonometry provide the foundations for calculus, and volition become especially important as we tackle more than advanced calculus topics.

Allow'due south go started.

What you need to know earlier yous get started: A brief tour of Calculus Pre-Requisites
Photograph by Dino Reichmuth, some rights reserved.

Tutorial Overview

This tutorial is divided into three parts; they are:

• The Concept of a Part
• Fundamentals of Pre-Algebra and Algebra
• Fundamentals of Trigonometry

The Concept of a Role

A part is a rule that defines the relationship betwixt a dependent variable and an independent variable.

Examples are all around united states of america: The average daily temperature for your city depends on, and is a office of, the time of year; the distance an object has fallen is a function of how much fourth dimension has elapsed since you dropped it; the surface area of a circle is a function of its radius; and the force per unit area of an enclosed gas is a function of its temperature.

– Folio 43, Calculus for Dummies, 2016.

In motorcar learning, a neural network learns a function by which it can represent the relationship between features in the input, the independent variable, and the expected output, the dependent variable. In such a scenario, therefore, the learned function defines a deterministic mapping between the input values and i or more output values. We can represent this mapping as follows:

Output(s) = function(Inputs)

More formally, however, a role is ofttimes represented by y = f(x), which translates to y is a function of x. This notation specifies 10 as the independent input variable that we already know, whereas y is the dependent output variable that we wish to find. For example, if we consider the squaring function, f(x) = ten ², and so inputting a value of 3 would produce an output of 9:

y = f(3) = 9

A office can also exist represented pictorially by a graph on an ten–y coordinate plane.

By the graph of the function f we mean the collection of all points (x, f(x)).

– Page 13, The Hitchhiker'due south Guide To Calculus, 2019.

When graphing a function, the independent input variable is placed on the x-centrality, while the dependent output variable goes on the y-axis. A graph helps to illustrate the relationship between the independent and dependent variables meliorate: is the graph (and, hence, the relationship) rising or falling, and by which rate?

A directly line is one of the simplest functions that can be graphed on the coordinate plane. Take, for example, the graph of the line y = iiix + 5:

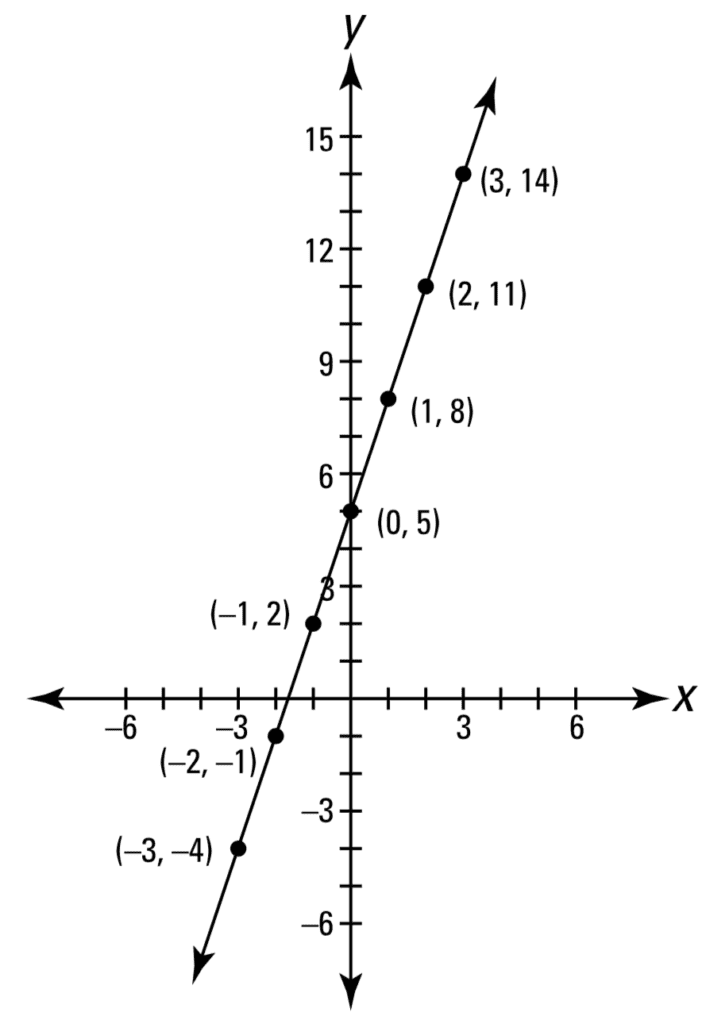
Line Plot of a Linear Function
Taken from Calculus for Dummies

This straight line tin can be described past a linear office, so called because the output changes proportionally to whatsoever change in the input. The linear function that describes this directly line can exist represented in slope-intercept class, where the gradient is denoted past g, and the y-intercept by c:

f(x) = mx + c = threex + 5

We had seen how to summate the slope when nosotros addressing the topic of Charge per unit of Alter.

If we had to consider the special case of setting the slope to zero, the resulting horizontal line would be described by a constant function of the form:

f(ten) = c = 5

Within the context of motorcar learning, the adding defined by such a linear part is implemented by every neuron in a neural network. Specifically, each neuron receives a set of north inputs, ten _i , from the previous layer of neurons or from the training data, and calculates a weighted sum of these inputs (where the weight, due west _i , is more common term for the gradient, m, in auto learning) to produce an output, z:

The Weighted Sum of Inputs
Taken from Deep Learning

The procedure of preparation a neural network involves learning the weights that best correspond the patterns in the input dataset, which process is carried out by the slope descent algorithm.

In add-on to the linear office, there exists another family of non-linear functions.

The simplest of all non-linear functions can be considered to be the parabola, that may exist described past:

y = f(x) = 10 ⁱⁱ

When graphed, nosotros find that this is an even part, because it is symmetric about the y-axis, and never falls beneath the x-centrality.

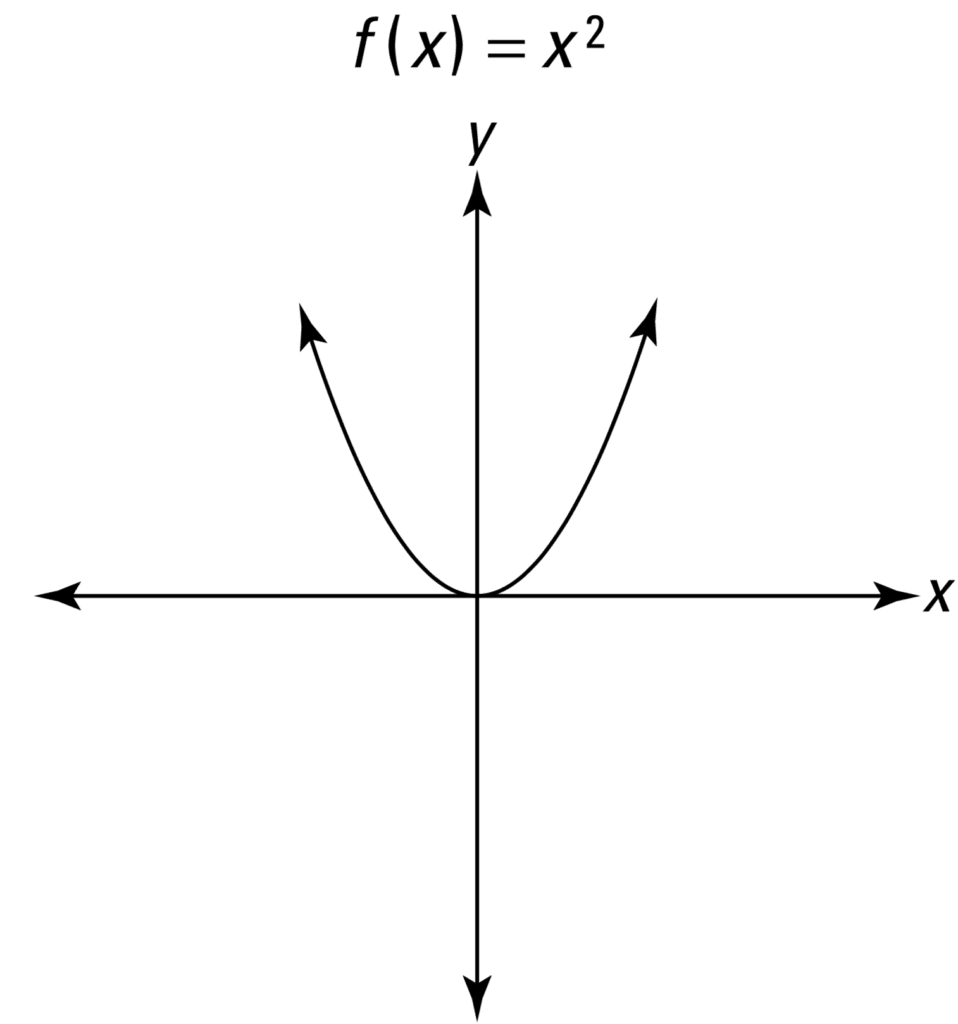
Line Plot of a Parabola
Taken from Calculus for Dummies

Nonetheless, non-linear functions can take many different shapes. Consider, for case, the exponential function of the grade f(x) = b ^x , which grows or decays indefinitely, or monotonically, depending on the value of x:

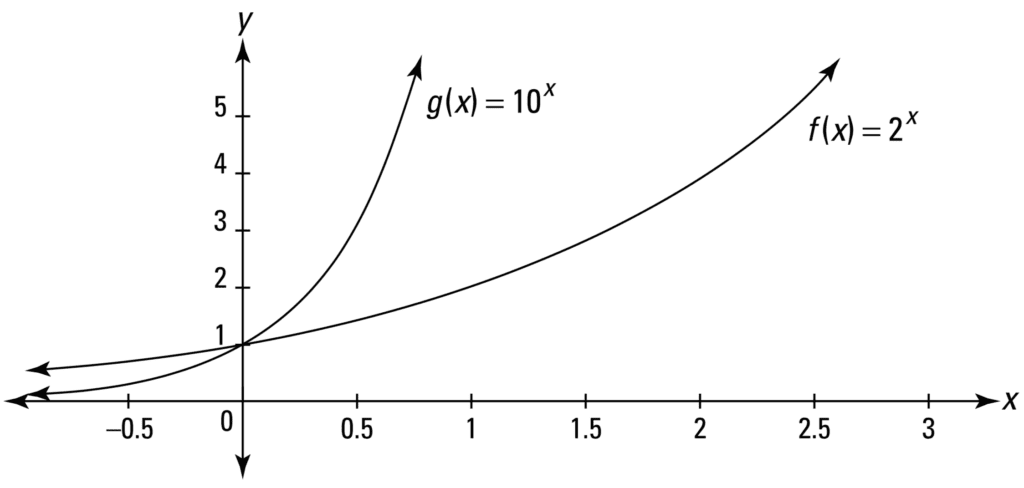
Line Plot of an Exponential Function
Taken from Calculus for Dummies

Or the logarithmic function of the class f(ten) = log ₂ ten, which is similar to the exponential part merely with the x– and y-axes switched:

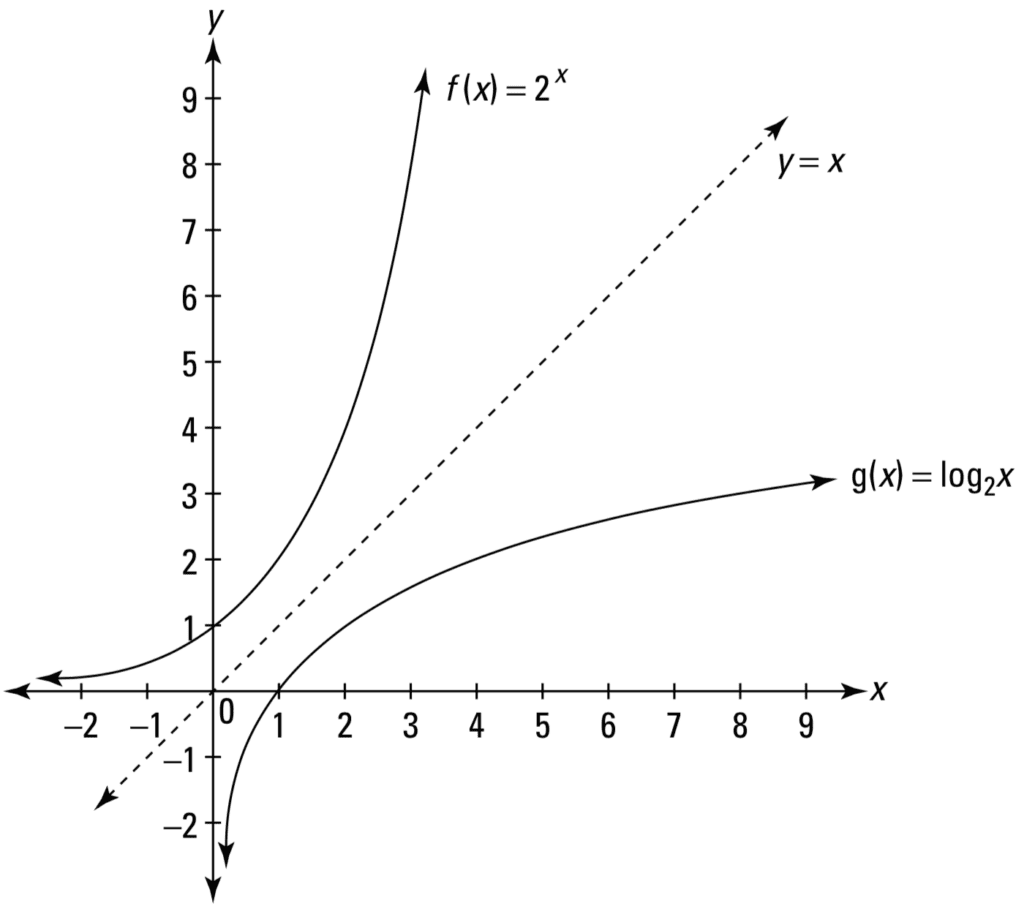
Line Plot of a Logarithmic Role
Taken from Calculus for Dummies

Of particular involvement for deep learning are the logistic, tanh, and the rectified linear units (ReLU) non-linear functions, which serve every bit activation functions:

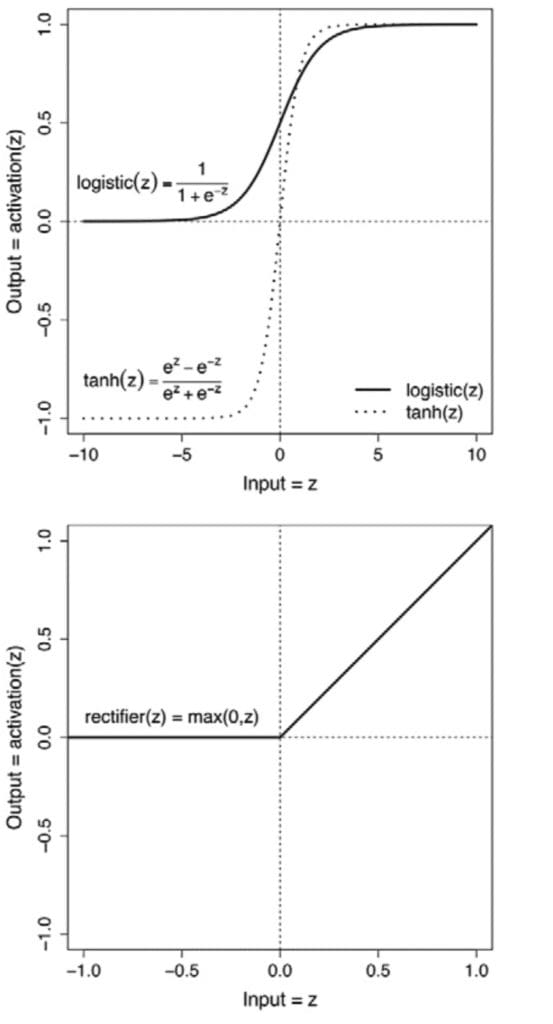
Line Plots of the Logistic, Tanh and ReLU Functions
Taken from Deep Learning

The importance of these activation functions lies in the introduction of a non-linear mapping into the processing of a neuron. If we had to rely solely on the linear regression performed by each neuron in calculating a weighted sum of the inputs, then we would be restricted to learning only a linear mapping from the inputs to the outputs. Notwithstanding, many real-world relationships are more than circuitous than this, and a linear mapping would not accurately model them. Introducing a non-linearity to the output, z, of the neuron, allows the neural network to model such non-linear relationships:

Output = activation_function(z)

… a neuron, the primal edifice cake of neural networks and deep learning, is defined past a unproblematic two-step sequence of operations: calculating a weighted sum and then passing the result through an activation office.

– Page 76, Deep Learning, 2019.

Non-linear functions announced elsewhere in the process of preparation a neural network too, in the course of error functions.

A non-linear mistake function can be generated by computing the error between the predicted and the target output values as the weights of the model change. Its shape can be every bit simple every bit a parabola, but virtually ofttimes it is characterised by many local minima and saddle points. The slope descent algorithm descends this not-linear mistake function past calculating the slope of the tangent line that touches the curve at some particular example: another of import concept in calculus that permits usa to analyse complex curved functions by cut them into many infinitesimal straight pieces arranged alongside 1 another.

Fundamentals of Pre-Algebra and Algebra

Algebra is one of the important foundations of calculus.

Algebra is the linguistic communication of calculus. Yous can't do calculus without knowing algebra any more than you can write Chinese poetry without knowing Chinese.

– Folio 29, Calculus for Dummies, 2016.

In that location are several fundamental concepts of algebra that turn out to be useful for calculus, such as those concerning fractions, powers, foursquare roots, and logarithms.

Let'due south first start by revising the basics for working with fractions.

• Segmentation past Zero: The denominator of a fraction can never be equal to zero. For case, the result of a fraction such as 5/0 is undefined. The intuition behind this is that you lot can never add together up the value in the numerator, using multiples of the zero in the denominator.
• Reciprocal: The reciprocal of a fraction is its multiplicative changed. In simpler terms, to find the reciprocal of a fraction, flip it upside down. Hence, the reciprocal of 3/4, for instance, becomes 4/3.
• Multiplication of Fractions: Multiplication betwixt fractions is as straightforward as multiplying across the numerators, and multiplying across the denominators:

(a / b) * (c / d) = air conditioning / bd

• Segmentation of Fractions: The division of fractions is very like to multiplication, but with an additional step; the reciprocal of the 2d fraction is first found before multiplying. Hence, considering again two generic fractions:

(a / b) ÷ (c / d) = (a / b) * (d / c) = ad / bc

• Addition of Fractions: An important first pace is to discover a common denominator between all fractions to be added. Any common denominator volition do, but nosotros usually find the least common denominator. Finding the least common denominator is, at times, as simple as multiplying the denominators of all individual fractions:

(a / b) + (c / d) = (ad + cb) / bd

• Subtraction of Fractions: The subtraction of fractions follows a similar procedure as for the addition of fractions:

(a / b) – (c / d) = (ad – cb) / bd

• Cancelling in Fractions: Fractions with an unbroken concatenation of multiplications beyond the entire numerator, also as beyond the unabridged denominator, can be simplified by cancelling out any mutual terms that appear in both the numerator and the denominator:

aⁱⁱⁱb² / ac = a²bⁱⁱ / c

The next important pre-requisite for calculus revolves around exponents, or powers as they are as well commonly referred to. There are several rules to go on in mind when working with powers likewise.

• The Power of Zero: The consequence of whatever number (whether rational or irrational, negative or positive, except for null itself) raised to the power of zero, is equal to one:

x⁰ = one

• Negative Powers: A base of operations number raised to a negative ability turns into a fraction, but does not change sign:

10^-a = i / x^a

• Fractional Powers: A base number raised to a partial power can be converted into a root problem:

ten^a/b = (^b√x)^a = ^b√x^a

• Improver of Powers: If two (or more) equivalent base terms are being multiplied to ane some other, then their powers may be added:

x^a * x^b = x^{(a + b)}

• Subtraction of Powers: Similarly, if two equivalent base terms are being divided, then their power may be subtracted:

10^a / 10^b = x^{(a – b)}

• Power of Powers: If a power is also raised to a power, then the two powers may be multiplied by one another:

(10^a)^b = x^(ab)

• Distribution of Powers: Whether the base numbers are existence multiplied or divided, the power may be distributed to each variable. Yet, it cannot be distributed if the base numbers are, otherwise, beingness added or subtracted:

(xyz)^a = 10^a y^a z^a

(x / y)^{a =} x^a / y^a

Similarly, we have rules for working with roots and rules for working with logarithms:

Properties of Roots
Taken from Calculus for Dummies

Properties of Logarithms
Taken from Calculus for Dummies

Finally, knowing how to solve quadratic equations can also come up in handy in calculus.

If the quadratic equation is factorable, then the easiest method to solve information technology is to express the sum of terms in production grade. For instance, the following quadratic equation tin be factored as follows:

x² – 9 = (x + iii)(x – 3) = 0

Setting each factor to cipher permits us to find a solution to this equation, which in this instance is 10 = ±3.

Alternatively, the following quadratic formula may be used:

The Quadratic Formula
Taken from Calculus for Dummies

If nosotros had to consider the aforementioned quadratic equation equally to a higher place, then we would set the coefficient values to, a = 1, b = 0, and c = 9, which would once again result in 10 = ±three as our solution.

Fundamentals of Trigonometry

Trigonometry revolves around three main trigonometric functions, which are the sine, the cosine and the tangent, and their reciprocals, which are the cosecant, the secant and the cotangent, respectively.

When applied to a right angled triangle, these iii main functions permit us to calculate the lengths of the sides, or whatsoever of the other two acute angles of the triangle, depending on the data that we have available to start off with. Specifically, for some angle, x, in the following 3-4-5 triangle:

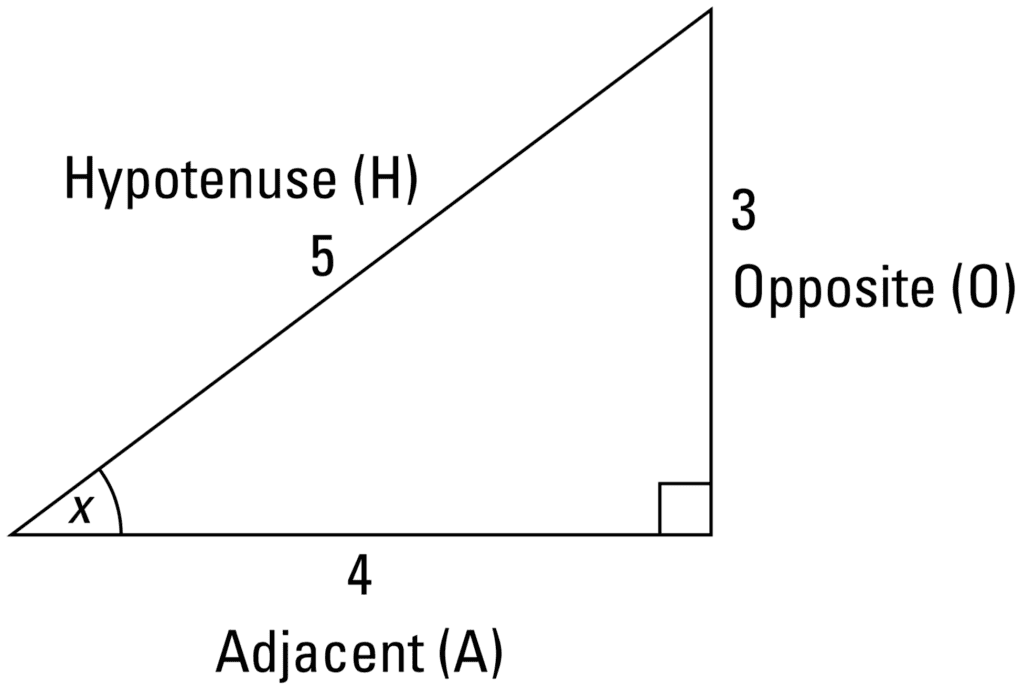
The 3-4-5 Triangle
Taken from Calculus for Dummies

The 3 Main Trigonometric Functions
Taken from Calculus for Dummies

The sine, cosine and tangent functions only work with right-angled triangles, and hence can just be used in the calculation of acute angles that are smaller than 90^o. All the same, if nosotros had to piece of work within the unit circle on the 10–y coordinate plane, then nosotros would be able to apply trigonometry to all angles betwixt 0^o and 360^o:

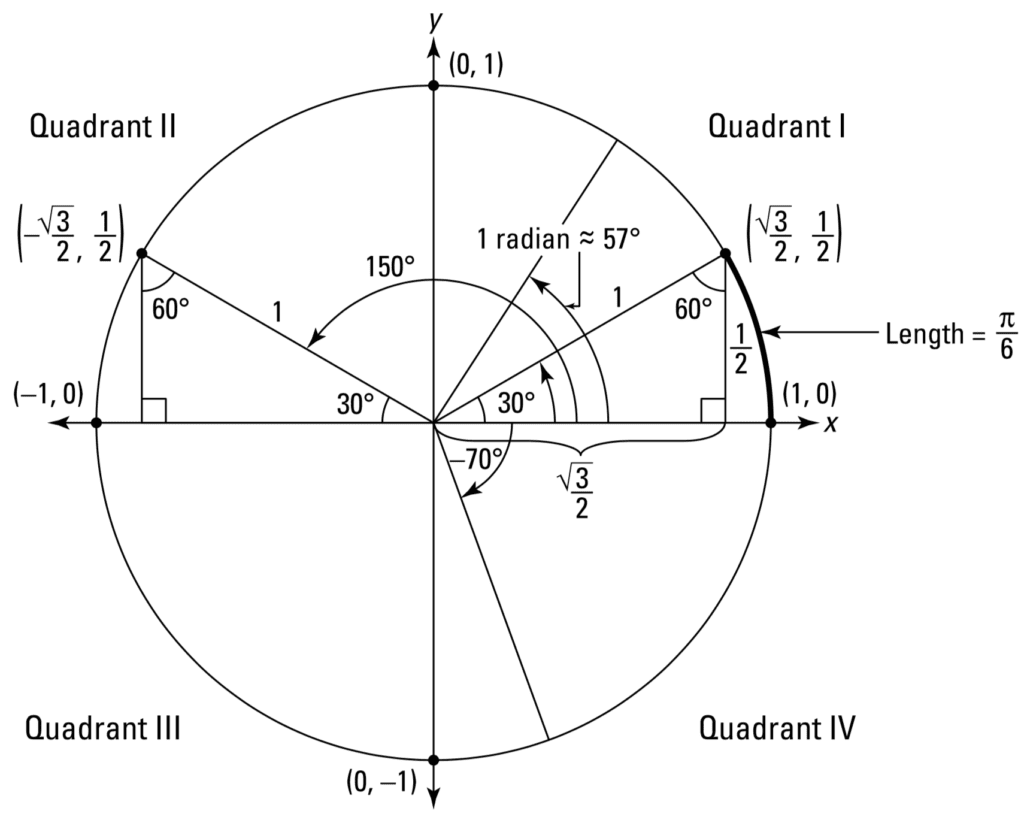
The Unit Circle
Taken from Calculus for Dummies

The unit circle has its center at the origin of the x–y coordinate plane, and a radius of one unit. Rotations around the unit of measurement circle are performed in a counterclockwise manner, starting from the positive x-axis. The cosine of the rotated angle would then exist given by the x-coordinate of the indicate that hits the unit circumvolve, whereas the y-coordinate specifies the sine of the rotated bending. It is likewise worth noting that the quadrants are symmetrical, and hence a point in one quadrant has symmetrical counterparts in the other 3.

The graphed sine, cosine and tangent functions appear as follows:

Line Plots of the Sine, Cosine and Tangent Functions
Taken from Calculus for Dummies

All functions are periodic, with the sine and cosine functions featuring the aforementioned shape albeit being displaced past xc^o between one another. The sine and cosine functions may, indeed, be hands sketched from the calculated ten– and y-coordinates as one rotates around the unit circle. The tangent function may also exist sketched similarly, since for any bending 𝜃 this function may exist defined by:

tan 𝜃 = sin 𝜃 / cos 𝜃 = y / x

The tangent function is undefined at ±ninety^o, since the cosine in the denominator returns a value of zero at this angle. Hence, we draw vertical asymptotes at these angles, which are imaginary lines that the bend approaches but never touches.

One final note concerns the inverse of these trigonometric functions. Taking the sine function every bit an example, its inverse is denoted by sin^-one. This is not to be mistaken for the cosecant function, which is rather the reciprocal of sine, and hence not the aforementioned as its inverse.

Further Reading

This department provides more resources on the topic if you are looking to go deeper.

Books

• Deep Learning, 2019.
• Calculus for Dummies, 2016.
• The Hitchhiker's Guide to Calculus, 2019.

Summary

In this tutorial, yous discovered several pre-requisites for working with calculus.

Specifically, yous learned:

• Linear and non-linear functions are central to calculus and machine learning, and many calculus problems involve their use.
• Fundamental concepts from algebra and trigonometry provide the foundations for calculus, and will become especially of import equally we tackle more advanced calculus topics.

Practise you have any questions?
Ask your questions in the comments beneath and I will exercise my best to reply.

Get a Handle on Calculus for Motorcar Learning!

Experience Smarter with Calculus Concepts

...by getting a ameliorate sense on the calculus symbols and terms

Find how in my new Ebook:
Calculus for Machine Learning

It provides self-study tutorials with full working code on:
differntiation, gradient, Lagrangian mutiplier arroyo, Jacobian matrix, and much more...

Bring But Enough Calculus Cognition to
Your Motorcar Learning Projects

Run across What'southward Inside

davisancestright.blogspot.com

Source: https://machinelearningmastery.com/what-you-need-to-know-before-you-get-started-a-brief-tour-of-calculus-pre-requisites/

Share this post